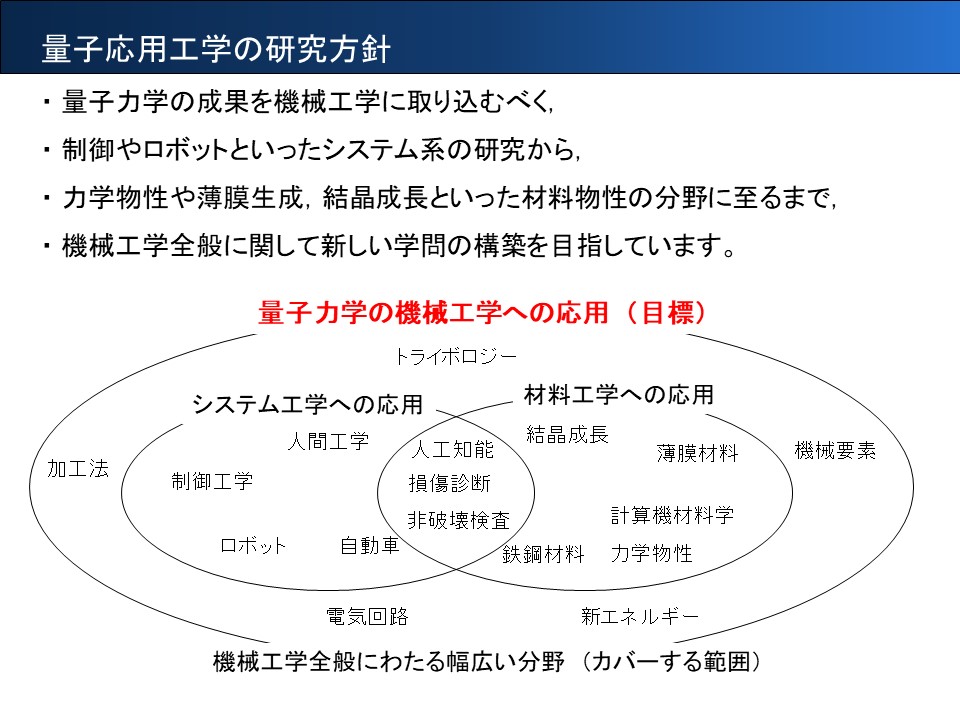
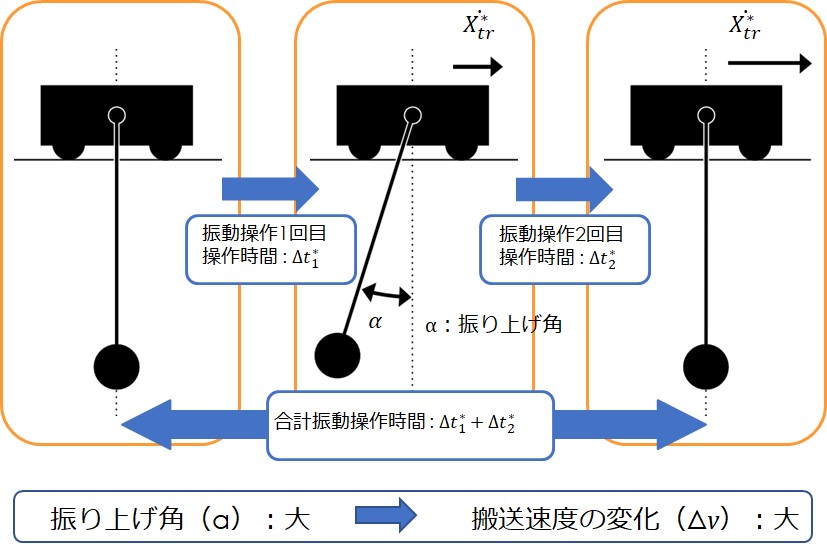
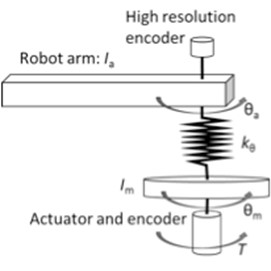
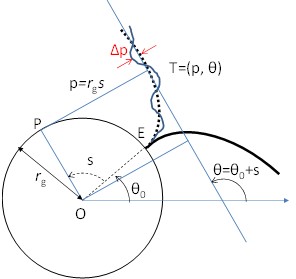
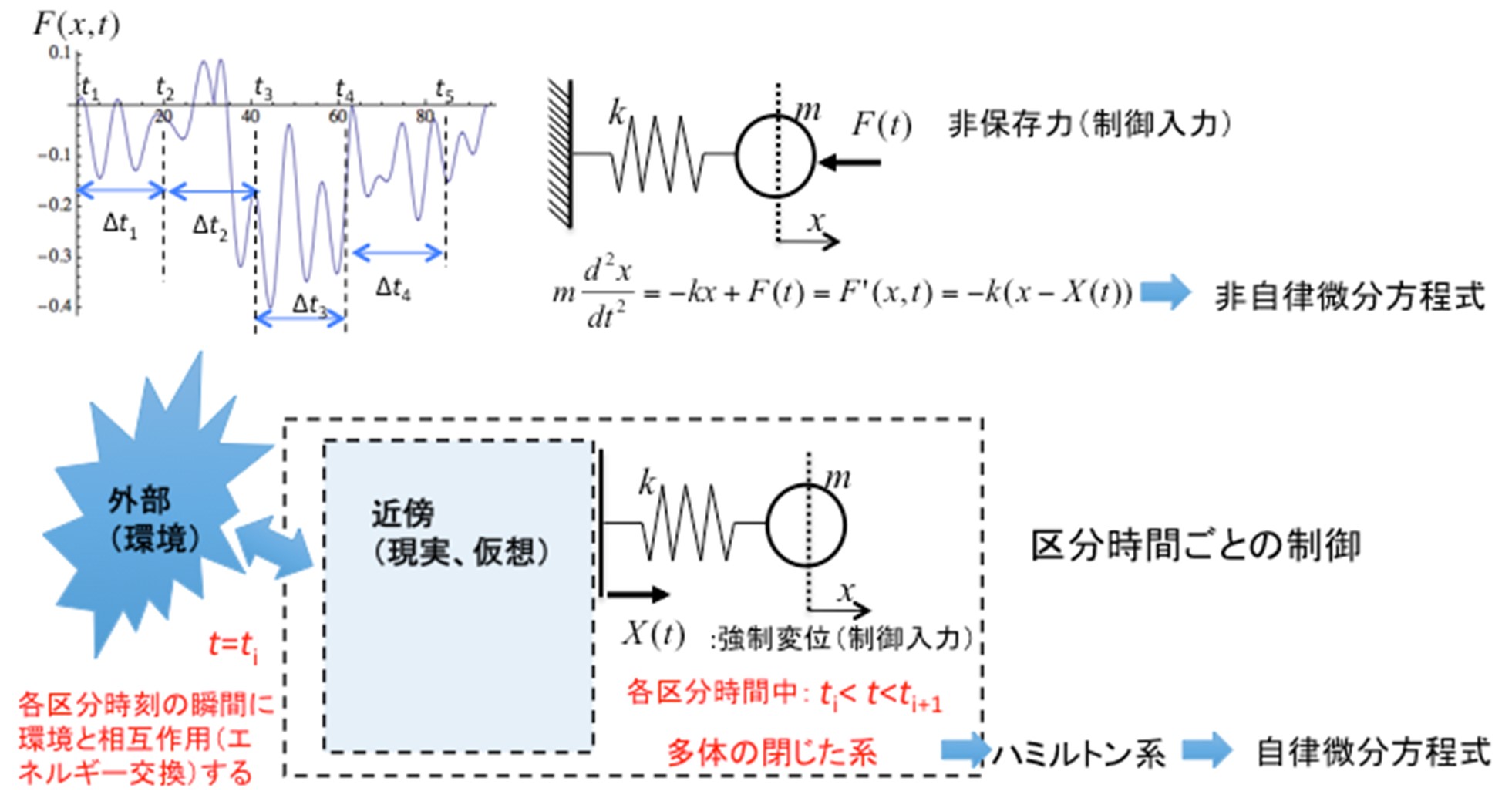
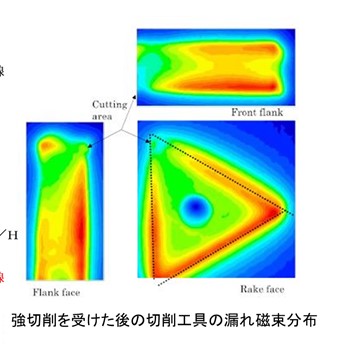
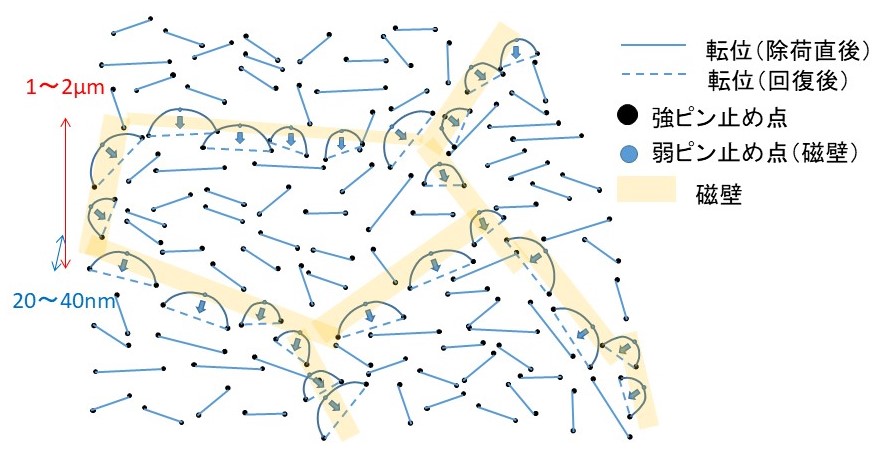
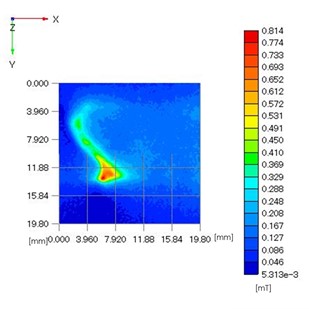
量子論の機械工学への応用
ニュートン力学と量子力学
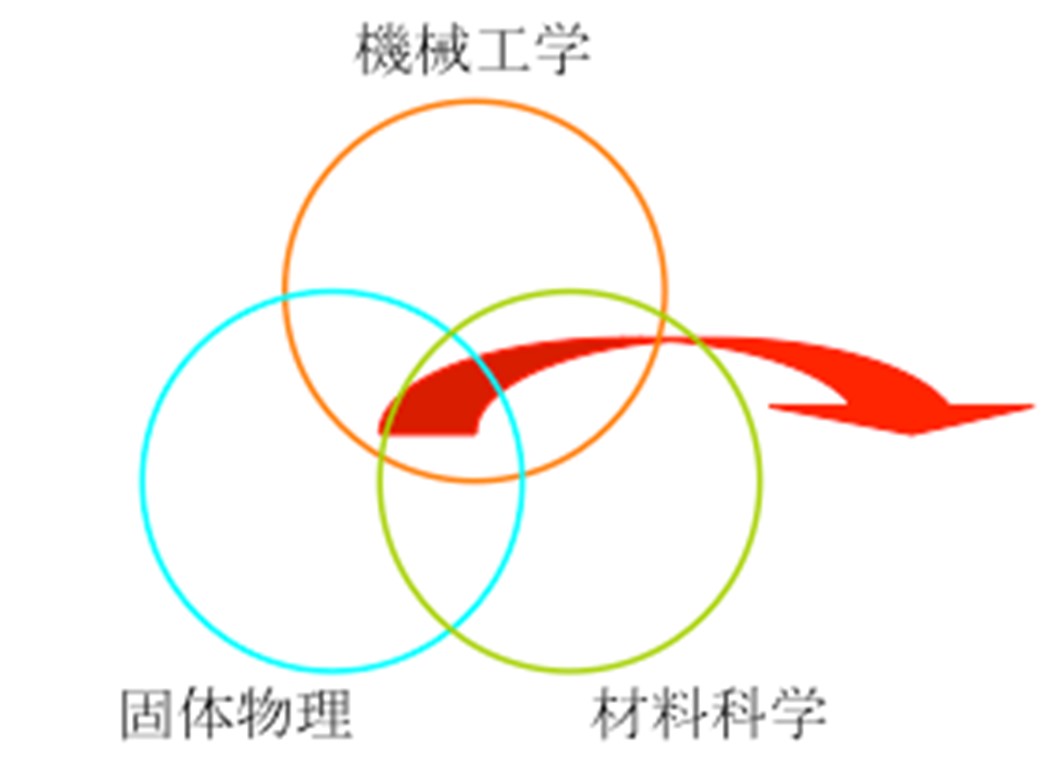
量子力学が誕生して,100年近くが経ちました.そんな中,電気電子における半導体や化学工学における分子軌道法などにおいて,この学問は大きな進展を支えてきました.ところが,機械工学は,依然としてニュートン力学を中心に構成されており,それがさらに発展した解析力学や量子力学を応用することはありませんでした.機械を人の思いの通り設計し操作する機械工学は,力に重きを置くニュートン力学と親和性が良く,それで十分だったのかもしれません. 一方,解析力学や量子力学は,自然の摂理を理解する手段として発展してきましたが,エネルギー的に閉じた系での振る舞いは,人為的な操作を常とする機械工学とは相いれないものでした. しかしながら,これらの3つは決して別々のものではなく,時間を追って前者から後者へと一般化され発展してきた以上, 機械工学入力においても進むべき一つの道であることには疑いはないでしょう.
近年における量子力学の発展
100年の時を経て,近年,量子力学は大きな飛躍を遂げようとしています.その一つは,量子コンピューターに代表される量子論の情報理論への発展であり,もう一つは,マテリアル・インフォマティックに代表される物性計算の広がりです. 前者により,従来,古典コンピューターを中心に発展してきた機械制御(メカトロニクス)や人工知能は,量子情報を用いた発展の可能性が出てきました. また後者により,量子力学を用いて電子の振る舞いを解き明かす第一原理計算は身近なものとなり,世界中のエンジニアが使うツールとなりつつあります.
量子アルゴリズムの制御理論への応用 & 物性論を基礎とする力学現象の理解
そこで当研究室では,前者の観点から,量子アルゴリズムの制御理論への応用を,後者の観点から,物性理論としてはあまり解明されてこなかった力学現象の理解を進めています.これらの研究を通して,機械工学と量子論をつなぐ学問の構築に取り組んでいます.